Thuật toán Quick Sort
Quick
Sort là một thuật toán sắp xếp không còn xa lạ với chúng ta. Không khó để tìm
các tài liệu về Quick Sort, nhưng khá khó để hiểu Quick Sort một cách tường tận.
Trong bài viết này, mình sẽ phân tích thuật toán trên một cách chi tiết nhất
nhé. Nào bắt đầu thôi!
THUẬT
TOÁN
Cho một dãy số 9, -1, 0,
4, 7, 10, 6. Dùng thuật toán Quick Sort để sắp xếp dãy số trên. Sau khi sắp xếp,
kết quả cho ra sẽ là -1, 0, 4, 6, 7, 9,
10 là một dãy số tăng dần.
Gọi quickSort(arr, l, r)
là hàm của thuật toán với 3 thành phần:
arr: mảng chúng ta cần sắp
xếp
l, r: left và right, là
hai con số xác định phần nào của mảng arr dùng để sắp xếp
Để dễ hình dung hơn, ta
có ví dụ thế này
Cho arr là dãy số lúc
nãy. Như hình trên, ta thấy rằng l = 4, r = 6. Lúc đấy ta sẽ gọi hàm lúc nãy là
quickSort(arr, 4, 6), hàm này sẽ chỉ sắp xếp một phần của dãy số là 7, 10, 6.
Sau khi gọi hàm này sắp xếp, ta sẽ thu được dãy như sau
Trong quá trình tính toán
thì l và r mới có sự thay đổi. Còn như ban đầu khi gọi hàm, thì l và r chính là
giá trị đầu và cuối của mảng. Gọi hàm sẽ là quickSort(arr,0,arr.length-1)
Vì sao lại tồn tại l và r
thì về sau các bạn sẽ rõ.
Ta có một quy tắc sau: Nếu
l >= r thì ta không làm gì cả.
Thật vậy, vì nếu l = r
thì đoạn cần sắp xếp chỉ có 1 phần tử. Còn nếu l > r thì không tồn tại mảng
cần sắp xếp.
Gạch chân xanh đậm trong
hình thể hiện phần của mảng thực hiện sắp xếp. Mình đã vẽ 3 trường hợp để bạn dễ
hình dung.
Như thế thì code ban đầu
của mình sẽ như sau:
Tiếp theo, mình sẽ định
nghĩa và gọi hàm partition(arr, l, r). Hàm này trả về một con số gọi là pivot (chốt).
Mình sẽ giải thích cách nó hoạt động thế nào, nhưng tạm thời ta hãy hiểu như thế
này.
Vòng tròn vàng là pivot.
Giả sử ta chọn số 6 là pivot. Khi đó, sau khi hàm này thực hiện, nó sẽ chia mảng
đang xét từ L tới R thành 2 phần. Một phần bao gồm các số nhỏ hơn pivot, phần
còn lại bao gồm các số lớn hơn pivot.
Ta thấy rằng -1, 0, 4 là
các số nhỏ hơn pivot; 9, 7, 10 là các số lớn hơn pivot
Sau khi chạy đoạn chương
trình, mảng sẽ thay đổi như sau
Bạn thấy rằng bên trái của
6 là các số nhỏ hơn 6, và bên phải của 6 là các số lớn hơn hoặc bằng 6. Ở đây
chúng ta không quan tâm đến thứ tự của chúng.
Sau khi chia làm 2 nhóm
thì bạn dễ nhìn thấy rằng số 6 nằm ngay đúng vị trí của nó. Như vậy số 6 là số
đã được sắp xếp.
Vậy thì nhiệm vụ của
chúng ta chỉ cần gọi hai hàm đệ quy. Một hàm cho nhóm bên trái, và một hàm cho
nhóm bên phải.
Cơ bản thì hàm sẽ viết
như thế này:
Việc chúng ta cần làm bây
giờ là giải quyết bài toán partition(). Làm sao để chia mảng thành hai phần như
trên?
Có khá nhiều cách để làm
được thế này. Nó phụ thuộc vào việc chọn pivot cũng như ý tưởng của mỗi người. Mình
sẽ chỉ một trong một số cách đó.
Giả sử với dãy số như
sau, cho pivot là phần tử cuối (=10). Ta quy định từ 0 đến i là các số nhỏ hơn
pivot (gạch xanh), các số từ i + 1 đến j là các số lớn hơn hoặc bằng 10 (gạch đỏ).
Ban đầu j = 0, thông qua thuật toán j = 5 (ta xét quá trình giữa của thuật toán
để nhìn thấy tổng quát).
Bây giờ tăng j = j + 1 =
6
Theo nguyên tắc trên thì
3 có vẻ không nằm trong khu vực màu đỏ vì 3 < 10. Nhiệm vụ của chúng ta là
chuyển nó sang khu vực màu xanh. Để làm được điều đó, ta sẽ thay số 13 và số 3,
sau đó tăng i lên 1 đơn vị
Sau khi hoàn thành thì j
tiếp tục chạy lên.
Đối với phần tử cuối cùng
là pivot, chúng ta thay vị trí của pivot và vị trí của i + 1.
Và cuối cùng chúng ta
cũng đã tìm được vị trí đúng của pivot, và chia mảng thành 2 phần (ta không cần
tăng j lên nữa vì mục tiêu của chúng ta đã đạt được)
Có một số cách khác các bạn
có thể khám phá, đại loại như sau:
Đây là lựa chọn pivot là
phần tử giữa, i chạy từ trái sang, j chạy từ phải sang. Về định nghĩa thì giống
nhau (vùng xanh nhỏ hơn pivot, vùng đỏ lớn hơn pivot). Về thuật toán thì các bạn
có thể tự suy nghĩ (mình đưa ra ý tưởng thui :D).
Thôi không dài dòng nữa,
chúng ta đi vào thực hiện thuật toán nào.
Trong code mình đã giải
thích ở note khá chi tiết rồi, nên ở đây không giải thích thêm nữa nhé!
Kết hợp 2 code ở trên, ta
sẽ chạy được kết quả của đề bài ban đầu như sau:
Còn một cái chúng ta cần
xem xét nữa là độ phức tạp của thuật toán. (Bạn nào chưa biết cách tính độ phức
tạp thì xem hai bài trước nhé)
ĐỘ
PHỨC TẠP
Quick sort là một hàm đệ
quy. Để dễ dàng cho việc xét độ phức tạp, ta chỉ cần xét trường hợp tốt nhất và
xấu nhất.
Trường
hợp xấu nhất: Mảng
đã được sắp xếp
Ví dụ: [1, 2, 3, 4, 5, 6,
7]
Với ví dụ trên, n = 7 thì
số lần gọi hàm sẽ như sau:
quickSort(arr, 0, 6)
-> quickSort(arr, 0, 5),... quickSort(arr, 0, 1)
n -> n – 1 -> n – 2
-> ... -> 1
Tổng của dãy số này sẽ là
n*(n-1)/2. Nhìn vào biểu thức ta có thể đoán được độ phức tạp là O(n2)
Trường
hợp tốt nhất:
Mỗi lần tìm pivot thì nó luôn nằm vị trí chính giữa
Ví dụ: [-2, 3, -1, 5, 4,
-3, 0]
Khi ta tìm pivot, thì nó
luôn nằm chính giữa hoặc cận giữa, và luôn chia đều hai bên.
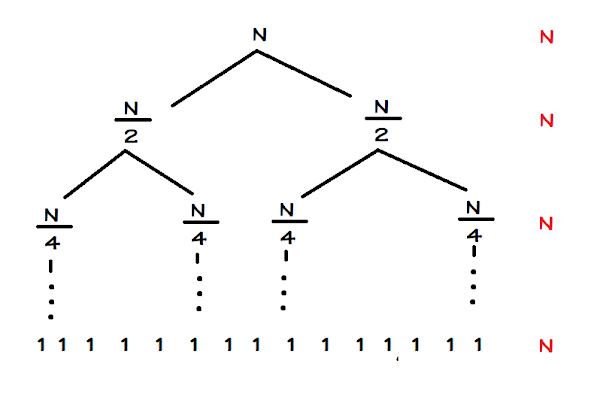
Ban đầu là 1 vòng lặp duyệt
n lần, sau đó là 2 vòng lặp duyệt n/2, tới 4 vòng lặp duyệt n/4... cho đến khi
còn 1. Ta có thể để ý rằng tổng các hàng cộng lại luôn bằng N (màu đỏ bên phải).
Nếu gọi x là số bậc của cây nhị phân trên thì trường hợp này có độ phức tạp là
O(x*n). Vậy tìm x như thế nào. Hãy xem phân tích sau
Ta thấy rằng x gần như thể
hiện cho vị trí của nó trong bậc của cây. Ví dụ với n/2 thì x = 1, bậc 2; n/4 thì
x= 2, bậc 3. Như thế thì ta sẽ giả sử x chính là vị trí của bậc trong cây (ta
giả sử vì bậc chính xác chỉ hơn x 1 đơn vị, không đáng kể đối với n cực lớn)
Với n/(2x) =
1. Thì ta sẽ tính như sau
Việc gọi log2(n)
hay log(n) cũng không ảnh hưởng gì đến kết quả.
Vậy độ phức tạp của thuật
toán trong trường hợp tốt nhất là O(nlogn)
Với trường hợp trung bình
cũng sẽ là O(nlogn) (Cách tính mình vẫn chưa tìm ra được :3)
Lời kết: Như
vậy là đã xong rồi đó. Thế là cuối cùng chúng ta cũng biết tường tận thuật toán
Quick Sort, cũng như là có thể tự ứng biến thuật toán theo ý thích của mình.
Ngoài ra chúng ta còn phân tích cả độ phức tạp của nó, hay phải không nào. Cảm
ơn các bạn đã theo dõi nhé!
Nội dung bài viết thuộc về Lê Công Diễn.Có sự
tham khảo từ CS Dojo!
Người
viết: Lê Công Diễn
Mang
đi nhớ ghi nguồn

















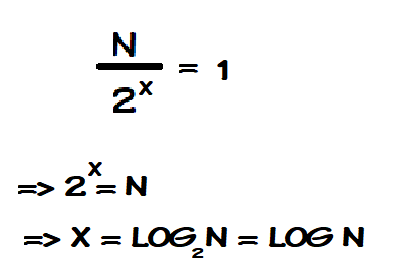
Nhận xét
Đăng nhận xét