Tìm hiểu về vector một cách dễ hiểu và chi tiết

 

Tìm hiểu về vector một cách dễ hiểu và chi tiết

Bạn đã từng học và nghe qua về Vector, nhưng bạn đã thực sự hiểu chúng chưa. Hãy cùng mình tìm hiểu nhé!

Trước khi định nghĩa Vector là gì thì chúng ta hãy nhớ thử xem khi người ta nhắc về Vector, bạn liên tưởng về cái gì:

-        Là một mũi tên với con số thể hiện trên đó

-        Hay đôi khi nó còn là 1 ma trận 1 cột

è Thực ra thì vector bao gồm cả hai cái đó, nó có chung một định nghĩa, nhưng sẽ có những cách biểu diễn khác nhau.

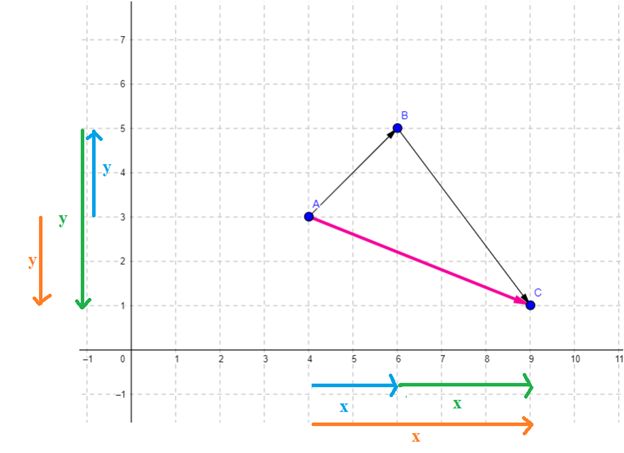
Cho một điểm A(4, 3) như hình

Ta muốn di chuyển A đến tọa độ (6,5). Trong lúc này, ta muốn có một phép toán nào đó đại loại A(4, 3) + alpha = A(6,5). Alpha này gọi là Vector.

 

Bạn để ý rằng nó giống như một hướng dẫn di chuyển cho điểm vậy. Để hướng dẫn một gì đó di chuyển tới vị trí nào đó, ta thường sẽ xác định 2 thông tin, thứ nhất đó là hướng, và thứ hai đó là độ lớn (số bước đi).

Theo như định nghĩa trên, ta có thể hoàn toàn gọi một Vector v(20^o, 2.5) để thể hiện rằng vật phải quay ở góc 20^o và đi 2.5 bước.

Tuy nhiên, thông thường người ta thường hay sử dụng Vector v(x, y) hơn, với x là số bước đi theo trục x và y là số bước đi theo trục y. Ví dụ như hình trên A(4, 3), ta cộng với alpha là Vector v(2, 2), thì:

-        A(4, 3) đi qua x 2 bước thành A(6, 3)

-        A(6, 3) đi qua y 2 bước thành A(6, 5)

Như thế A(4, 3) + v(2, 2) = A(6, 5).

Ta có thể kết luận đại khái là vector là một bảng hướng dẫn mà khi cộng với một thứ gì đó hay điểm nào đó ở vị trí nào đó thì vật đó sẽ chuyển sang vị trí mới.

Một ví dụ rất quen thuộc mà bạn không hề để ý đó chính là thời gian. Trong thời gian cũng tồn tại khái niệm điểm và vector. Ta có thể xem thời gian như đồ thị một chiều. Mốc thời gian là điểm, còn khoảng thời gian là Vector.

Ví dụ: Mình đang ở trong lớp học lúc 13h30’, mình bỗng quay sang hỏi bạn bên cạnh.

-        Uầy, mấy giờ mới hết tiết vậy mày, lâu quá.

-        Một tiếng nữa mày ạ!

Biểu diễn trong đồ thị thì mốc thời gian M(13h30’) và Vector v(1h). Còn nếu mình hỏi rằng “Thầy vào lớp lúc nào thế?; 1 tiếng trước” thì Vector sẽ là v(-1h).

Biểu diễn kiểu ma trận thực chất cũng chỉ giống như dạng v(x, y) phía trên.

VD:

 => di chuyển theo trục x 2 bước sang bên phải, sau đó di chuyển song song với trục y xuống dưới 3 bước.

Ta có một số quy tắc sau:

-        Vector + Vector = Vector

-        Điểm + Vector =  Điểm 

-        Điểm + Điểm = Không tồn tại

Vector có thể cộng Vector, và sẽ tạo ra một vector mới. Giống như việc bạn cộng “1 tiếng nữa” và “2 tiếng nữa” sẽ thành “3 tiếng nữa” vậy đấy. Nhưng điểm + điểm thì sẽ không tồn tại, hai mốc thời gian cộng cho nhau thì chẳng có ý nghĩa gì cả.

 

Đại khái cũng hiểu cơ bản rồi đó. Tiếp đến, ta cùng tìm hiểu hai phép toán trong vector: Cộng vector và nhân vector

Cộng vector:

Ta nhìn hình sau

Ở mức độ trực quan, ta thấy rằng vector AB + vector BC = vector AC. Vì:

A đi theo vector AB sẽ tới điểm B, và đi theo vector BC sẽ tới điểm C

A đi theo vector AC sẽ tới điểm C

Như thế tổng 2 vector trên = vector dưới.

Ở mức độ toán học, ta thấy rằng:

Xét theo trục x. Khi x của vector AB (xanh dương) khi cộng x của vector BC (xanh lá) sẽ ra x của vector AC (cam) (chỉ là cộng hai số thôi). Điều này tương tự với y.

Từ đó ta có thể kết luận hai ý:

Vector AB + Vector BC + Vector CD + ... + Vector XY + Vector YZ = Vector AZ

v1(x₁, y₁) + v2(x₂, y₂) + v3(x₃, y₃) + ... + vn(x_n, y_n) = v(x₁ + x₂ + ... + x_n, y₁ + y₂ + ... + y_n)

Đối với ma trận:

Ta làm tương tự như cách tính trên: Lấy từng hàng cộng với nhau.

Nhân hai vector:

Nhân vector chính là sự kéo co dãn vector đó. Như hình trên thì vector v đã được kéo dãn gấp đôi, tạo thành vector mới lớn hơn vector cũ 2 lần.

Ở phép nhân, vector mới chỉ thay đổi về độ lớn.

Hmm, chưa hẳn, vì nếu nó nhân với hệ số âm thì sao? Nó sẽ quay hướng ngược lại với hướng cũ. Như vậy phép nhân vector chỉ thay đổi độ lớn và có thể thay đổi hướng nhưng chỉ hướng ngược lại mà thôi. Mình nghĩ bạn có thể dễ dàng hiểu nó nên mình sẽ không cần phải nói thêm.

Quá trình kéo dãn hoặc co hoặc đảo hướng vector này gọi là scaling

Các hệ số 2, 1/3,... được gọi là scalars

Đối với ma trận:

Các số trong ma trận gọi là coordinates

Ở ma trận ta chỉ việc lấy scalar nhân với từng số trong ma trận.

Điều này tương tự với Vector dạng v(x, y). Ta có a*v(x, y) = v(x*a, y*a) (Bạn có thể chứng minh tại sao khi scale x và y với hệ số a thì độ dài vector cũng sẽ scale theo hệ số a thông qua công thức Pytago, mình muốn chứng minh cho các bạn xem lắm mà sợ sẽ dài dòng nên thôi nhé!)

Dựa vào đây, người ta nghĩ ra một cách biểu diễn khác cho vector: Coi các hệ số trong ma trận là các scalar. Sử dụng hai vectors cơ bản i-hat và j-hat.

Hai vector này là vector cơ bản. Cơ bản tức là từ nó bạn tạo ra được nhiều thứ, ở đây là tạo ra vector. Bạn đặt hướng nào cũng được, trừ một số trường hợp đặt biệt. Thông thường người ta đặt i ở trục hoành và j ở trục tung.

Bằng việc scale hai vector này, ta có thể tạo ra bất kỳ vector nào trong không gian.

Bạn có thể để ý trong hình thì vector màu đỏ được tạo ra từ việc kéo dãn hai vector hệ số màu hồng i và j (Lưu ý là vector dù ở vị trí nào cũng như nhau cả nhé).

Vector đỏ là tổng hai vector xanh dương, với hai vector xanh dương được tạo thành từ việc scaling hai vector cơ bản màu hồng.

 

Lâu lâu bạn sẽ thấy người ta hay vẽ vector nằm ở gốc tọa độ, đó là thường người ta hay biểu diễn kiểu này. Nó vẫn đúng nha vì theo quy tắc cộng khi trượt vector -2j qua bên phải thì sẽ ra thôi.

 

Với cách biểu diễn này thì các số trong ma trận đều hiểu là scalar hết

Nếu viết dưới dạng phép toán thì sẽ như hình trên!

Lời kết: Coi như chúng ta đã hiểu một cách sơ bộ về vector rồi đấy. Việc hiểu rõ vector giúp các bạn vận dụng linh hoạt cho các bài toán (biểu diễn vector dưới dạng nào cũng tùy vào bài toán cụ thể mà lựa chọn cho phù hợp nữa nhé).

 Nội dung bài viết thuộc về Lê Công Diễn. Có sự tham khảo và sử dụng một vài hình ảnh từ 3Blue1Brown (ảnh màu đen đen í vì lười vẽ haha:D).

 

Người viết: Lê Công Diễn

Mang đi nhớ ghi nguồn