Machine
Learning cho người ngố
Phần 1: Linear Regression
Mình
đang dự định làm một series về Machine Learning. Không hẳn là sẽ có nhiều thời
gian làm về cái này, nhưng sự hứng thú của mình về nó sẽ là động lực lớn để
mình cố gắng thêm.
Bạn có
thấy tiêu đề bài viết của mình có gì khác lạ không? Cho người ngố? Cụm từ tiếng
Anh của nó là “for dummies”. Bạn sẽ phát hiện ra rằng cụm từ này xuất hiện nhiều
trong các tựa đề cuốn sách “Design Pattern for Dummies”, “ English Grammar for
Dummies”,… cụm từ này có nghĩa là ngay cả khi bạn ngu ngốc thì vẫn có thể đọc
được. Và đó cũng chính là mục tiêu của mình khi viết bài blog, làm sao để mọi
người có thể đọc được.
Các
bài viết trên mạng đều sử dụng khá nhiều thuật ngữ và được viết một cách bài bản,
vì họ là người chuyên đi nghiên cứu. Còn mình khi viết bài sẽ cố gắng đứng trên
góc độ của các bạn, và giải thích rõ những thuật ngữ, cũng như dùng lời văn gần
gũi nhất. Nào cùng bắt đầu nhé!
Phần đầu
tiên chúng ta sẽ tìm hiểu về Linear Regression. Nó nằm trong nhóm Supervised
Learning (Học có giám sát)[*]. Để hiểu rõ hơn về Linear Regression
là gì, ta có ví dụ sau:
(Dữ liệu
thể hiện sự tương quan giữa Tuổi (x) và Mức chi tiêu trung bình cho y tế (y))
Bạn có
thể thấy rằng, tuổi càng tăng, thì mức chi tiêu càng tăng theo. Như ví dụ ở tuổi
15 là 100, 25 là 135, 40 là 250.
Bạn thử
chấm các điểm này lên đồ thị hai chiều nhé (Những cái cơ bản về đồ thị mình sẽ
không nói nhiều để tránh lan man)
Bạn có
cảm giác rằng các điểm này nó đi theo một đường thẳng không?
Các điểm
này có xu hướng nằm gần đường thẳng mà chúng ta vẽ ra. Đường thẳng này gọi là đồ
thị tuyến tính (Linear Graph).
Ở trên
hình, chúng ta có được phương trình đường thẳng y = 16.891x – 355.32. Giả sử ta
có độ tuổi là 30, ta đặt x0 = 30. Thế x0 vào phương trình
trên, sẽ là y0=16.891*30 – 355.32 = 151.41. Như vậy chúng ta đoán rằng,
với người 30 tuổi thì chi tiêu y tế trung bình sẽ là 151.41
Và
chúng ta ước rằng giá như chúng ta biết phương trình của đường thẳng này với y
= f(x), chỉ cần ta bỏ x vào là chúng ta có thể đoán được giá trị y.
Và
phương trình đường thẳng có dạng là y = ax + b, trong không gian ba chiều là y
= ax + bz + c, không gian bốn chiều là y = ax + bz + cm + d. Từ đó bạn có thể
suy ra phương trình tuyến tính trong không gian n chiều rồi nhỉ. (Số chiều đại
diện cho số lượng thuộc tính, với bài toán trên có hai cột thuộc tính sẽ là hai
chiều, ba cột sẽ là ba chiều,…)
Gọi m
= n – 1. Ta có phương trình tuyến tính không gian n chiều là
Nhiệm
vụ chúng ta là tìm được phương trình này đúng không? Mà tìm phương trình chính
là tìm hằng số w0, w1, w2,…, wm để
tạo được phương trình hoàn chỉnh.
Giả sử
chúng ta nhìn bằng mắt thường, và kẻ một đường thẳng mà chúng ta cho là ổn.
Thì, chúng ta sẽ như sau
Có quá
nhiều đường thẳng mà chúng ta đều cảm thấy rằng là nó “ổn”. Vậy đâu là đường thẳng
mà chúng ta lựa chọn?
Chúng
ta sẽ đánh giá nó dựa trên khoảng cách của từng điểm dữ liệu đến phương trình
đó, cụ thể như hình sau:
Nếu tổng
khoảng cách giữa các đường thẳng đen này là nhỏ nhất, thì khi đó phương trình
(đường thẳng) đó sẽ là phương trình tối ưu.
Thế,
câu hỏi đặt ra: Làm sao để tính được đường thẳng này
Xét một
điểm nhất định trong tập dữ liệu mẫu: x0 = 70, y0 = 1500
(trong bảng Excel ở hình trên).
Nhiệm
vụ của ta là tìm con số này
Con số
này chính là f(x0), nghĩa là mình thay x0 vào phương
trình trên thì sẽ ra con số ? trong hình.
Và cuối cùng mình sẽ lấy hiệu hai số này |y0 – f(x0)|. Đây chính là khoảng cách từ 1 điểm đến đường thẳng. Vậy khoảng cách tổng các điểm đến đường thẳng là
Trong
không gian nhiều chiều, công thức này vẫn giữ nguyên, vì khoảng cách này mình
chỉ xét trục y, không quan tâm số chiều.
Lưu ý:
xk không phải là vị trí x thứ k trong phương trình f(x), mà là dữ liệu
x dòng thứ k trong tập dữ liệu train: xk = (x1, x2,
x3,…, xm) [xk là một bộ số]
L(w)
chính là kí hiệu thể hiện tổng khoảng cách giữa các điểm đến đường thẳng
Người
ta có điều chỉnh hàm L(w) sao cho phù hợp và dễ dàng trong việc tính toán
Ở đây,
người ta chia cho n để lấy giá trị trung bình, mục tiêu để tránh giá trị L(w)
quá lớn. Việc giảm giá trị hàm L(w) không ảnh hương đến bài toán, vì mục tiêu của
chúng ta là chọn L(w) nhỏ nhất, nên không cần phải chính xác.
Số 2
trong 1/(2n) để thuận tiện trong quá trình đạo hàm (lát nữa bạn sẽ thấy)
Trong
hàm tổng có sử dụng phép bình phương. Hàm bình phương là một hàm mũ. Với hàm mũ
y = x2 (x>0), nếu giá trị x càng lớn, thì y càng tăng.
Nếu ta
sử dụng hàm mũ, thì với mỗi điểm dữ liệu, khoảng cách (x) càng lớn, thì kết quả
nhận được (y) càng cao theo cấp số mũ. Người ta làm vậy để tăng sự chênh lệch
giữa các đường thẳng đen mình đã vẽ, để dễ dàng lựa chọn hơn.
Ta thống
nhất chọn hàm L(w) được điều chỉnh nhé.
Trước
khi đi tiếp, mình sẽ nhắc lại thêm một lần nữa. Mục tiêu chúng ta là tìm w0,
w1, w2,…, wm để xây dựng được phương trình.
Cách
đơn giản nhất mình có thể nghĩ ra tại thời điểm này là chọn random các w trong
k lần lặp để thế vào L(w), rồi mình sẽ lựa L(w) nhỏ nhất để lấy các hệ số w. Nó
cũng là một cách, nhưng khá là mang tính ngẫu nhiên. Vì thế, chúng ta cần lựa
chọn các w nhưng phải có nguyên tắc.
Bạn thấy
rằng, phương trình L(w) là một phương trình bậc hai (lại bậc hai nhé :D), mà bạn
thấy được dạng của bậc hai, như hình lúc nãy bạn xem.
Phương
trình này đã chọn 1 điểm wi làm biến số, các wj với j≠i
còn lại thì là hằng số.
Mục
tiêu của mình có phải là kiếm L(w) nhỏ nhất đúng không? Mà L(w) nhỏ nhất khi nằm
ở điểm G.
Vậy
làm sao chọn wi sao cho L(w) đạt ở điểm G.
Ta biết
rằng tại điểm G thì đạo hàm L(w) sẽ bằng 0 với wi là biến. Bạn có thể
hiểu ý nghĩa đạo hàm như thế này:
Đạo
hàm tại một điểm nào đó mà có giá trị dương, thì lúc đó tại hai điểm gần nhất của
điểm đó sẽ tăng.
Trong hình
là mình đã phóng to lên tại điểm wi, thì tại điểm đó đồ thị đi lên,
lúc đó đạo hàm sẽ dương.
Tương
tự đạo hàm âm, nghĩa là tại điểm đó, đồ thị đi xuống.
Với đạo
hàm bằng 0, đồ thị tại điểm đó sẽ nằm ngang
Như thế,
ta chỉ cần tìm điểm mà L(w) = 0 thì đó sẽ là điểm tối ưu.
Tuy
nhiên điểm L(w) = 0 là rất khó để đạt được, vì thế chúng ta sẽ chọn L(w) nhỏ nhất
mà ta cảm thấy ổn.
Ban đầu,
chúng ta sẽ chọn wi bất kỳ, sau đó chúng ta sẽ thực hiện như sau:
-
Với đạo hàm L(w) với biến wi mà > 0 thì ta sẽ
giảm wi
-
Với đạo hàm L(w) với biến wi mà <0 thì chúng
ta sẽ tăng wi
Chúng
ta cứ tăng, giảm với cường độ nhỏ dần, nhỏ dần cho đến khi wi chạm
sát đến điểm G thì dừng lại.
Chúng
ta có công thức thay đổi wi như sau:
Đầu
tiên cần giải thích một chút về kí hiệu![]() , đây là ký hiệu đạo hàm của hàm số L(w) trên biến wi. Khi xưa, các bạn học đạo hàm, chỉ có thể
thấy như thế này L’(w) thôi đúng không. Đây cũng là kí hiệu của đạo
hàm, nhưng theo biến x. Các bạn biết rằng, với các biến không được xét đạo hàm
sẽ được xem như hằng số. Và ở đây, vì chúng ta không đạo hàm cho biến x nên cần
phải ghi rõ ra.
, đây là ký hiệu đạo hàm của hàm số L(w) trên biến wi. Khi xưa, các bạn học đạo hàm, chỉ có thể
thấy như thế này L’(w) thôi đúng không. Đây cũng là kí hiệu của đạo
hàm, nhưng theo biến x. Các bạn biết rằng, với các biến không được xét đạo hàm
sẽ được xem như hằng số. Và ở đây, vì chúng ta không đạo hàm cho biến x nên cần
phải ghi rõ ra.
Tại
sao lại trừ biểu thức![]() ? Thứ nhất, λ là
một hệ số được người ta thêm vào để có thể tinh chỉnh được mức độ thay đổi của
wi (dễ hiểu mà đúng không, với λ cao thì wi thay đổi càng lớn, và λ nhỏ
thì wi thay đổi chậm (Đó là hệ số bạn tự chọn). Thứ hai,
? Thứ nhất, λ là
một hệ số được người ta thêm vào để có thể tinh chỉnh được mức độ thay đổi của
wi (dễ hiểu mà đúng không, với λ cao thì wi thay đổi càng lớn, và λ nhỏ
thì wi thay đổi chậm (Đó là hệ số bạn tự chọn). Thứ hai, ![]() là
giá trị xét dấu, tức là nó giúp chúng ta biết rằng wi đang nằm ở vị
trí đạo hàm âm hay dương để thực phép cộng hay trừ cho phù hợp (Dấu trừ phía
trước đạo hàm chính là để đảo dấu, đạo hàm âm gặp dấu trừ sẽ là cộng; đạo hàm
dương gặp dấu trừ sẽ là trừ).
là
giá trị xét dấu, tức là nó giúp chúng ta biết rằng wi đang nằm ở vị
trí đạo hàm âm hay dương để thực phép cộng hay trừ cho phù hợp (Dấu trừ phía
trước đạo hàm chính là để đảo dấu, đạo hàm âm gặp dấu trừ sẽ là cộng; đạo hàm
dương gặp dấu trừ sẽ là trừ).
Như
mục tiêu, thì chúng ta biết cách tính các wi rồi đấy. Ban đầu chúng
ta sẽ chọn n con số wi ngẫu nhiên. Với mỗi wi mình sẽ duyệt
cho tới khi nào giá trị wi hội tụ (giảm đến mức gần như không thể giảm
thêm), khi đó ta sẽ chọn wi đó làm hệ số cho phương trình f(x) ban đầu
của mình. Vậy là xong bài toán rồi đúng không?
À,
bạn còn thắc mắc rằng làm sao tính đạo hàm ![]() đúng không? Được rồi, chúng ta sẽ tính đạo hàm
cho đứa này. Nhưng, nếu bạn quên các công thức đạo hàm, thì mình sẽ note cho
các bạn ở bước nào dùng công thức nào. Vậy nhé, bắt đầu thôi!
đúng không? Được rồi, chúng ta sẽ tính đạo hàm
cho đứa này. Nhưng, nếu bạn quên các công thức đạo hàm, thì mình sẽ note cho
các bạn ở bước nào dùng công thức nào. Vậy nhé, bắt đầu thôi!
[0]:
Bạn chú ý hai chỉ số là k và i:
-
k là chỉ số của tổng, chỉ số khi duyệt tập dữ liệu đầu vào
-
i là chỉ số thể hiện vị trí thứ i trong phương trình
[1]:![]()
Với
f(x) là hàm số chứa biến x
[2]:
Với
a, k là hằng số, f(x) là hàm số chứa biến x.
[3]:
- Đưa 2 ra khỏi tổng
-![]()
Với
u và v là hàm số chứa biến đạo hàm
[4]: yk không phải biến đạo hàm nên được xem như là hằng số
[6]:
Các số hạng đều
là đạo hàm hằng (công thức [4]), ngoại trừ
đều
là đạo hàm hằng (công thức [4]), ngoại trừ![]() vì
nó có chứa biến đạo hàm
vì
nó có chứa biến đạo hàm ![]()
[7]![]()
Với
a là hằng số, x là biến đạo hàm.
Ở
đây a tương đương với![]() , x tương đương với
, x tương đương với![]()
Chúng
ta thế công thức đạo hàm vào lại phương trình trên
Đây
chính là công thức chúng ta dùng để tìm từng wi. Như vậy, các bước
thực hiện thuật toán như sau.
- B1:
Chọn random các wi (VD: w1 = 3, w2 = 5, w3
= 7,…)
- B2:
Duyệt từng wi :
+ Với mỗi wi sẽ thực hiện công
thức này cho đến khi wi hội tụ.
- B3: Thế
các wi vào phương trình f(x), ta thu được một phương trình hoàn chỉnh
Tuy
nhiên, với mỗi điểm w random lúc đầu khi chạy thuật toán sẽ cho ra kết quả
phương trình f(x) khác nhau. Chính vì thế chúng ta cần lặp lại thuật toán này
liên tục rồi lựa chọn phương trình f(x) nào có khả năng dự đoán tốt nhất.
Vậy là
chúng ta đã hiểu được rõ về Linear Regression rồi đấy. Mà đây chỉ là phương
trình đường thẳng (Linear) thôi. Đối với các dữ liệu có xu hướng đi theo cấp số
mũ, hoặc theo nguyên tắc khác thì việc sử dụng Linear dự đoán sẽ ra kết quả khá
thấp.
Trước
khi tiến hành tạo ra mô hình dự đoán, chúng ta cần phải lọc các dữ liệu gây ảnh
hưởng đến kết quả mô hình. Như hình dưới đây là những dữ liệu gây ảnh hưởng
Để lọc
được dữ liệu này chúng ta cần có một số kỹ thuật. Tuy nhiên trong bài viết này
sẽ không đề cập đến vấn đề đó.
Bài viết
đến đây là đủ dài rồi. Mình hi vọng phần sau mình sẽ viết code chi tiết cách thực
hiện cụ thể thuật toán này, từng bước một. Nhưng sẽ khó để hứa được, vì viết
bài về Machine Learning khá thú vị nhưng khá mất công. Bài viết này mình đã mất
8 tiếng để thực hiện được, chắc là bài viết khủng nhất mình từng viết (dài bằng
cái luận văn luôn T_T)
Hi vọng
các bạn sẽ thích!
Nội dung bài viết thuộc về Lê Công Diễn.
Người viết: Lê
Công Diễn
Mang đi nhớ ghi nguồn
[*] Ví
dụ bạn có những tấm hình về động vật. Bạn cho đứa trẻ học bằng cách chỉ vào cái
hình và dặn chúng đó là con chó, đó là con mèo,… Sau khi học xong, bạn dùng những
tấm hình khác về động vật, và hỏi chúng rằng đâu là con chó, đâu là con mèo. Đó
là học có giám sát. Còn học không có giám sát là việc ban đầu bạn cho chúng
hình về động vật, nhưng không chỉ chúng rằng đâu là con chó, hay con mèo. Hay
nói cách khác, học không giám sát là học với dữ liệu train ban đầu không được
đánh dấu thuộc tính phân lớp (không biết trước kết quả).




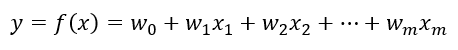


















Hay quá anh mấy kiến thức này khi e mới bắt đầu hơi bị khó khăn mất cả 1 tuần để hiểu nó.
Trả lờiXóaEm là sinh viên năm 2 trường Nông lâm cũng đang tìm hiểu về lĩnh vực này và muốn đi theo hướng NLP. Có gì anh cho e xin kinh nghiệm học hỏi vs ạ hihi :3
Giờ mới thấy tin nhắn em kk thông cảm nhé. Em còn tính năm cuối làm luận văn liên quan NLP không?
Xóa